
Once you abandon Newtonian physics and include general relativity, all possibility of a perfectly circular orbit goes out the window. That makes the orbit spiral either outward or inward.Ī spiraling orbit is not perfectly circular! This results in a non-radial component of force that either adds orbital energy to the other object or removes energy, depending on whether the angular rotation rate is faster or slower than the orbital rate. Rotation at a rate different from synchronous with the orbit then drags the long axes of the prolate spheroids away from pointing directly toward the other prolate spheroid's center. If they rotate at the same angular rate as they orbit, then the long axes of the prolate spheroids line up with each other and there is no non-radial (from the barycenter) component of gravitational force, so a circular orbit is possible. Assuming two bodies, their mutual tidal forces perturb their shapes into prolate spheroids - like rugby balls. If you allow non-rigid bodies (but keep Newtonian physics and an otherwise-empty universe), unless the bodies rotate at the same angular rate as they orbit (they are locked in terms of relative orientation), then tidal effects perturb the orbits. most models of the universe don't involve such geometry. For that matter, case 2 above is difficult to pull off, even in Newtonian physics, without resorting to electric charges to counter what gravity is trying to make them do. This works for Newtonian physics and special relativity, but as I said in a comment, I haven't pondered the implications of general relativity. That single case is actually a class of cases, in which 1) all the other mass in the universe is concentrated along the line normal to the bodies' orbit plane and passing through the barycenter, and 2) those masses are either static (non-moving) or moving in such a way that the net gravitational force at the orbit of the bodies in question doesn't change. What happens when you replace these ideological models with real-world realities?Īpart from a single case, as soon as you allow other mass in the universe, "perfect" goes out the window. This geometry was discussed in a science fiction novel some decades ago - Ringworld? I don't have time to look it up.īut the foregoing assumes three things that we know not to be true in the real world.

You don't have to specify just two bodies because under these assumptions theoretically you could have three or more such objects orbiting the barycenter in circular, coplanar orbits. The answer depends: how accurate is the physics you consider?Ĭonsidering the symmetric system postulated in other answers/comments, one with two spherically-symmetric bodies of equal masses, orbiting their barycenter: if you use only Newtonian physics, empty the universe of all masses other than the ones you're focusing on, and make the bodies perfectly rigid (i.e., ignore the physics of non-rigid bodies to maintain their spherical symmetry), then indeed theoretically you could have perfectly circular orbits. So you could get close to, but never achieve perfection. However, gravitational influence will always cause some minute eccentricity even if it is undetectable. If you had a perfectly even sphere far away from any other celestial bodies, say halfway between galaxies, and a spacecraft with an extremely accurate guidance and control system you could get close to perfection. No orbit can be perfect because the gravity of other celestial bodies will always cause a small amount of eccentricity. That isn't much, but it will have in influence Gravitational influence of other celestial bodies: my answer to this question shows that Jupiter's influence on a body in Earth orbit when the Earth and Jupiter are close together is 3.2e-7 m/second squared.Changes in the density of the orbited planet.Spacecraft system inaccuracy: no spacecraft is perfect, no matter how accurate.There will always be eccentricity in an orbit, even if it is very small.
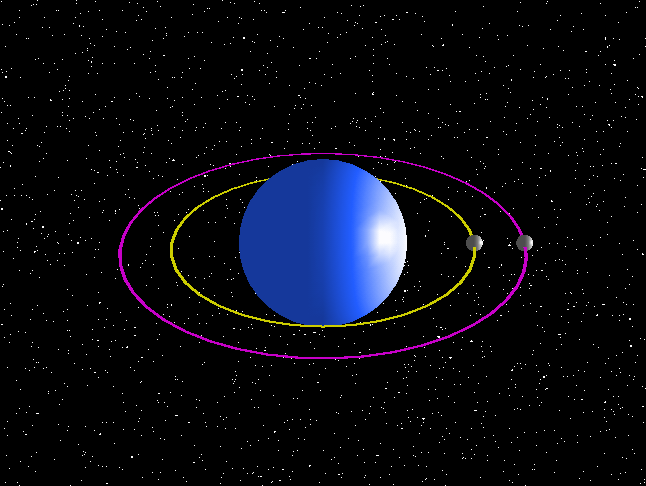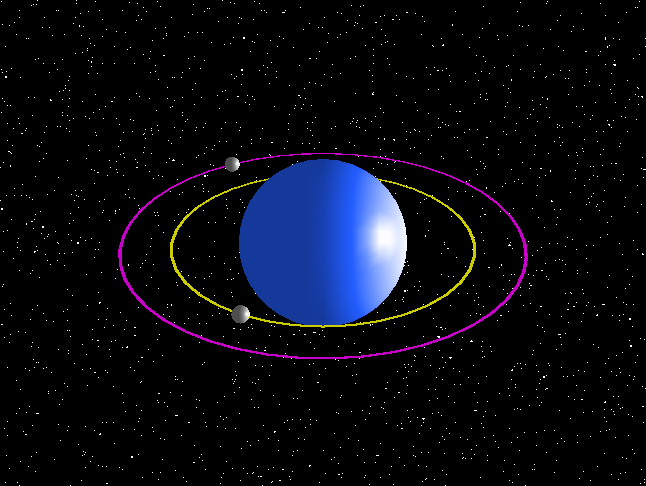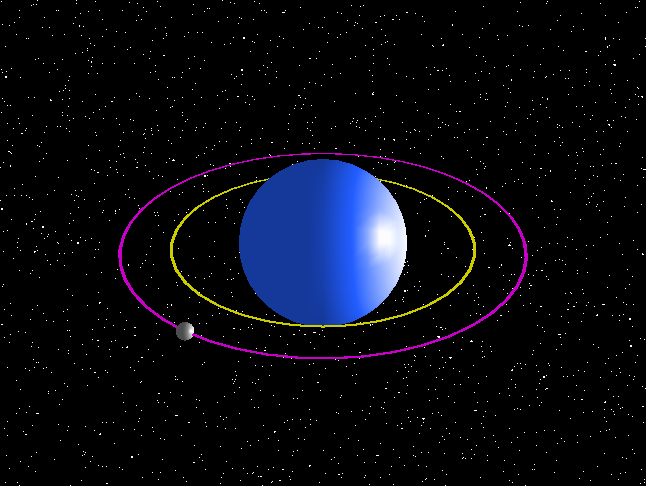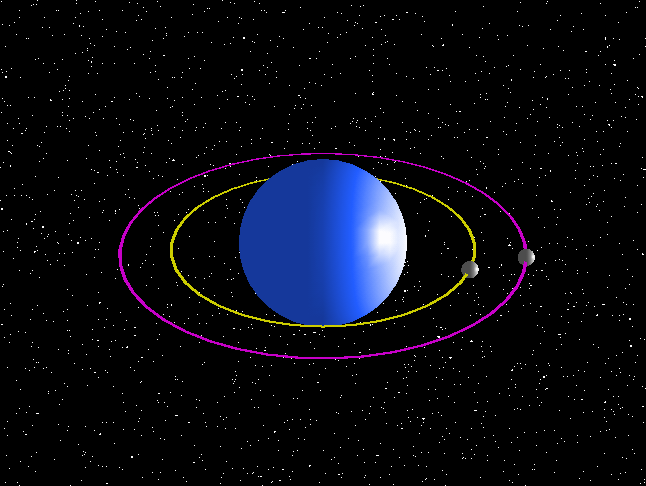
If you define perfection as absolutely zero eccentricity then perfection is impossible.


 0 kommentar(er)
0 kommentar(er)
